
Binary search algorithm example with PHP
Binary search with PHP
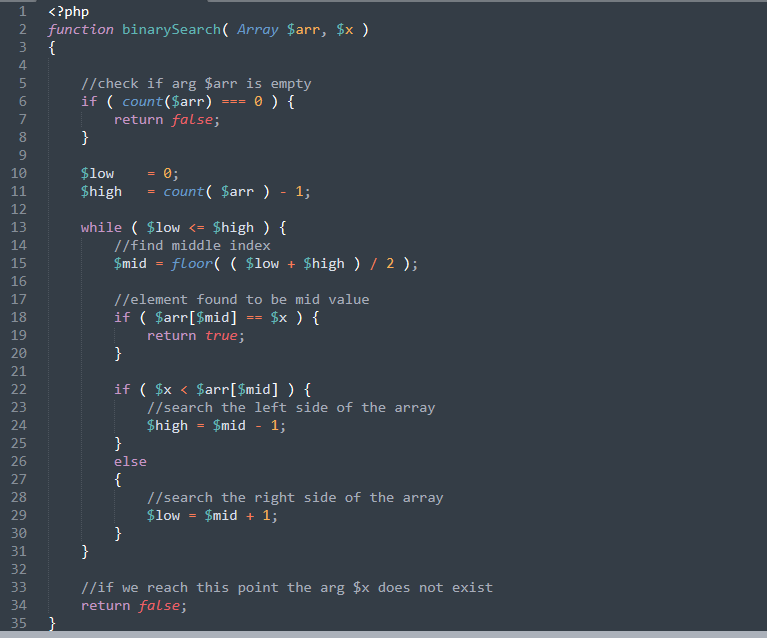
Binary search is perhaps the most famous search algorithm for sorted arrays in software development. Let's take a look how a simple binary search algorithm might look like in PHP. Hopefully at the end of this blog post you will understand why this is probably one of the most popular algorithm’s in software development and why it is used to quickly find a target value in a sorted sequence of values. I haven't used binary search too often in real life projects, but this is the algorithm that is really worth knowing and understanding ( that is if you are a developer, otherwise it's maybe better to not know about it at all ).
binary search code example
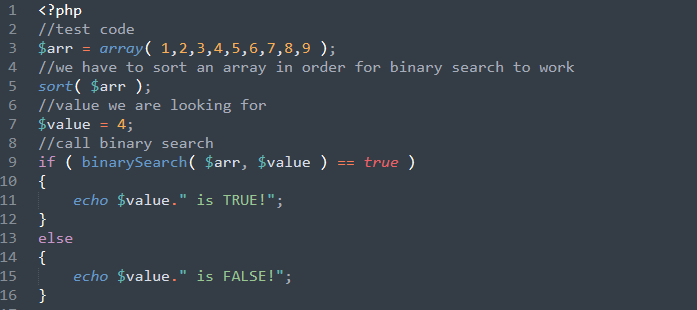
binary search - execution script
This algorithm is easy to implement and in the same time it is very fast. Binary Search is only possible on sorted arrays and that is probably it's only limitation. If there is a need for extracting data out of large sorted arrays, linear search, which is O(n) runtime, just won't cut it, and this is where binary search algorithm comes into play. Binary search is a divide and conquer algorithm, which means that it divides a large array into two smaller sub arrays and then iteratively ( or recursively ) operate on each sub array and reduces the search volume to half at each step. It discards one sub array and continues to work on the second sub array until it finds the value that it is searching for. This is possible because the original array is sorted and the algorithm knows where the middle value is at the beginning of the process.
Binary search runs in logarithmic time in the worst case, making O(log n) comparisons, where n is the number of elements in the array, the O is Big O notation, and log is the logarithm. Binary search takes constant O(1) space, meaning that the space taken by the algorithm is the same for any number of elements in the array.
Logarithmic runtime can be seen as the opposite of an exponential runtime O(N2) in the same way dividing is the opposite of multiplying for example. Therefore, Binary search as an logarithmic runtime algorithm increases logarithmically with the number of elements in the array it has to search which is opposite to exponential increase. O(N2) or exponential runtime, is common in algorithms that involve nested iterations over the array data sets. Deeper nested iterations can result in O(N3) or O(N4) and we can see how this can be a problem for Big Data and why logarithmic runtimes like Binary search which do the opposite, needs to be implemented. We can also see a nice example of recursive behavior in algorithms here, which is a pattern that is very important for algorithmic thinking. Try out this binary search example in your favorite code editor and see the results. You can use much bigger arrays for binary search, and this is where you can really see the real power of this amazing and yet simple algorithm.
Stay tuned and happy coding.








